Sparse Approximate Hamilton-Jacobi Solutions for Optimal Feedback Control with Terminal Constraints

Abstract

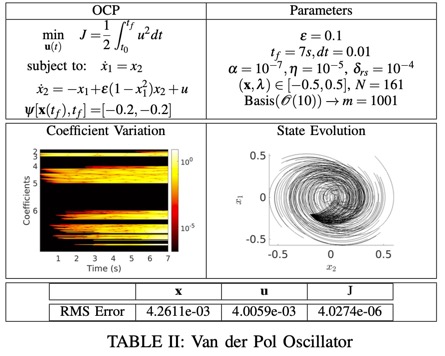
A semi-analytic method is proposed to solve a class of optimal control problems while exploiting its underlying Hamiltonian structure. Optimal control problems with a fixed final state at a fixed terminal time are considered. The solution methodology proposed in this work solves the Hamilton-Jacobi equation over a predefined domain of states and co-states. The advantage over traditional methods is that an approximate generating function (analogous to the value function of HJB theory) is obtained as a function of time, which allows for the computation of co-states for any final time and final state specified. Numerical experiments are conducted to demonstrate the efficacy of developed method while considering benchmark problems including spin stabilization.